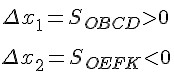СЛОБОДСКОВ БОРИС АНАТОЛЬЕВИЧ - ФИЗИКА (КУРС ЛЕКЦИЙ)

ЛЕКЦИИ ПО ФИЗИКЕ
Кинематика

§ 15. Графики зависимости модуля и проекции скорости равномерного прямолинейного движения от времени

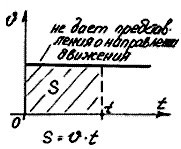
1. График модуля скорости.

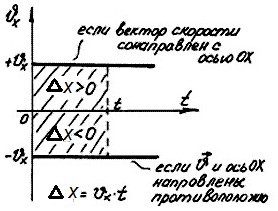
Знаем, что в равномерном прямолинейном движении = const, то есть не изменяется с течением времени. Следовательно, график зависимости скорости от времени - прямая, параллельная оси времени. Кроме того, модуль - неотрицательная величина, следовательно, эта прямая лежит выше оси времени.

Зная график модуля скорости, можно найти не только модуль скорости, но и путь S, пройденный точкой. Он численно равен площади прямоугольника, расположенного под графиком модуля скорости.

2. Графики проекции скорости.

Так как = const, то и = const. Поэтому графиками также будут прямые линии, параллельные оси времени. Но в отличие от модуля проекции могут быть как положительными, так и отрицательными. Поэтому графиком = f (t) является прямая, параллельная оси времени, которая может быть расположена как выше, так и ниже оси t.

   По графикам можно найти проекцию и модуль скорости. По знаку проекции скорости можно судить о направлении движения точки относительно оси OX. Если > 0, то вектор скорости точки сонаправлен с осью OX, и точка движется в положительном направлении оси. Если же < 0, то вектор скорости точки противонаправлен оси OX, и точка движется против положительного направления оси.
   Кроме того, по графикам проекции скорости можно найти изменение координаты движущейся точки.
   Знаем:

Тогда:

Изменение координаты движущейся точки численно равно площади прямоугольника между графиком проекции скорости и осью времени. Площади приписывают знак "плюс" или "минус". Если график расположен выше оси времени, то площадь считают положительной, и изменение координаты движущейся точки больше нуля. Если график расположен ниже оси времени, то площадь считают отрицательной, и изменение координаты движущейся точки меньше нуля.

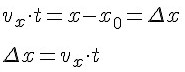< Предыдущий параграф < Оглавление > Следующий параграф >