|
ЛЕКЦИИ
ПО ФИЗИКЕ |
|
|
|
|
|
© Лопатин
Павел Борисович |
|
|
1. Постоянство ускорения. Таким же
способом, как и при движении тела,
брошенного горизонтально, легко
доказать, что это движение происходит с
ускорением свободного падения, которое
вблизи Земли постоянно по модулю и
направлению. Так как это движение с
постоянным ускорением Движение тела, брошенного под углом к горизонту - это второй пример криволинейного движения с ускорением свободного падения.
2. Нахождение времени подъёма до наивысшей точки и максимальной высоты подъёма.
Это время легко найти из формулы проекции скорости на ось OY, т.к. в наивысшей точке подъёма скорость направлена горизонтально, т.е. перпендикулярно оси OY, и её проекция на эту ось равна нулю.
Максимальную высоту подъёма найдём из уравнения координаты по оси OY.
3. Время полёта и время падения. Время
полёта находится из уравнения
координаты y.
Если точки бросания и падения не лежат на одном уровне, то эти соотношения не выполняются, но находить их также.
4. Дальность полёта, когда точки бросания и падения находятся на одном уровне. Для нахождения дальности полёта в уравнение координаты x надо подставить время полёта. Обратим внимание, что движение по оси OX - равномерное:
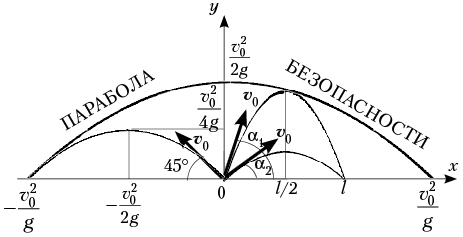
4а. Найдём угол, при котором дальность полёта при заданной начальной скорости будет наибольшей. 4б. Покажем,
что дальность полёта тел, брошенных под
углами
Действительно, если Таким
образом, дальность полёта тел,
брошенных по настильной траектории
(под углом В частности, это выполняется для углов 30 градусов и 60 градусов (см. рис. выше).
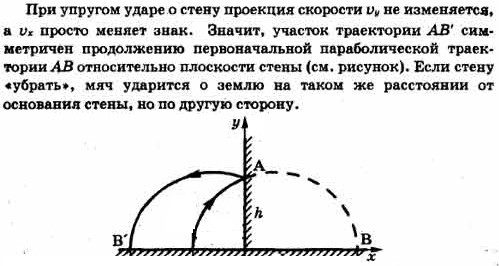
5. Упругий удар о стену тела, брошенного под углом к горизонту.
6. Понятие параболы безопасности.
Парабола безопасности - это линия,
такая, что все точки, лежащие вне неё, не
могут быть достигнуты телом (снарядом)
при заданной начальной скорости и
любом угле бросания (вывод формулы
параболы безопасности см. здесь
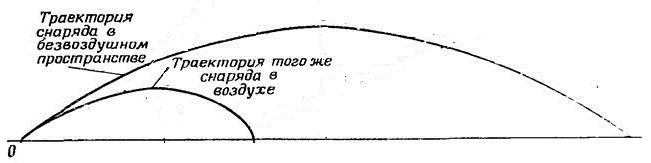
7. Баллистическая траектория. Изложенные выше формулы и рассуждения справедливы в том случае, если мы не учитываем сопротивление воздуха. В реальных ситуациях тела движутся по так называемым баллистическим кривым, или баллистическим траекториям, которые отличаются от правильной параболической формы.
Баллистическая траектория — это траектория, по которой движется тело, обладающее некоторой начальной скоростью, под действием силы тяготения и силы аэродинамического сопротивления воздуха. Форма участков баллистической траектории, проходящих в плотных слоях атмосферы зависит от многих факторов: начальной скорости тела, его формы и массы, текущего состояния атмосферы на траектории (температура, давление, плотность), направления вращения Земли и от характера движения тела вокруг его центра масс. Форма баллистической траектории в этом случае обычно рассчитывается методом численного интегрирования дифференциальных уравнений движения тела в стандартной атмосфере (условном вертикальном распределении температуры, давления и плотности воздуха в атмосфере Земли, принятом международной организацией по стандартизации).
8. Надо запомнить. 1) В точке
наивысшего подъёма
2) Движение по оси OX - равномерное, т.е. с постоянной скоростью
Движение по оси OY - равнопеременное: равнозамедленное
- до равноускоренное
- после 3) Если точки бросания и падения находятся на одном уровне, то
4) Если точки
бросания и падения находятся на одном
уровне, то направляющие косинусы в
точке бросания и точке падения
одинаковы 5) На одной и той же высоте (по вертикали) от точки бросания скорости подъёма и падения одинаковы, а также равны направляющие косинусы этих скоростей. 6) Наибольшая
дальность полёта при заданной
начальной скорости будет при угле
бросания 7) Дальность
полёта при углах бросания |
|
|
< Предыдущий параграф < Оглавление > Следующий параграф > Контрольная работа № 6 по теме "Движение тела, брошенного горизонтально и под углом к горизонту" |
|
|
 =const,
то оно происходит в одной плоскости, в
данном случае - в вертикальной
плоскости. Поэтому для решения любой
задачи достаточно знать два уравнения
координаты и два уравнения проекции
скорости.
=const,
то оно происходит в одной плоскости, в
данном случае - в вертикальной
плоскости. Поэтому для решения любой
задачи достаточно знать два уравнения
координаты и два уравнения проекции
скорости.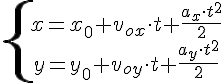 ;
;
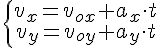

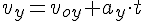
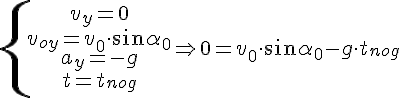
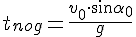
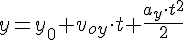
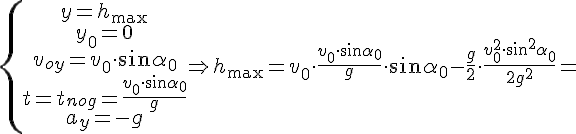
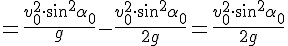

 ;
;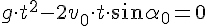 ;
;
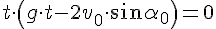
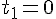 - момент бросания
- момент бросания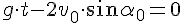 ;
;
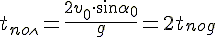
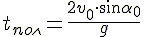
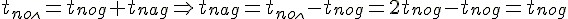
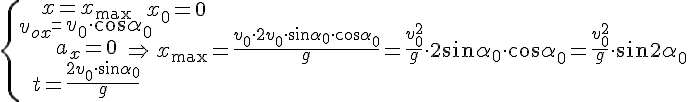
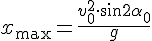
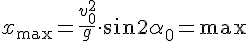 ,
если
,
если 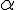 и
и 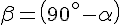 к горизонту, одна и та же.
к горизонту, одна и та же.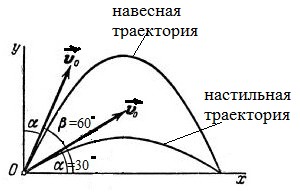
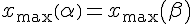 ,
то
,
то .
.