ЛЕКЦИИ ПО ФИЗИКЕ
Кинематика

© Лопатин Павел Борисович
Настоящий курс лекций построен на основе лекций, которые читал Б.А. Слободсков.

§ 18. Мгновенная скорость в переменном движении

1. Мгновенная скорость.

   В переменном движении скорость изменяется по модулю и направлению в каждое мгновение, поэтому уже нельзя говорить, что скорость в любой момент времени показывает, какое перемещение совершается за 1 секунду.

   Уменьшая неограниченно промежутки времени , будем получать средние скорости, которые всё меньше и меньше отличаются от скорости в точке M (см. рисунок выше). При неограниченном уменьшении промежутков времени () мы получим среднюю скорость, стремящуюся к истинной скорости тела в точке M.

Определение. Мгновенной скоростью переменного движения называется предел, к которому стремится отношение перемещения ко времени , за которое это перемещение произошло, когда промежуток времени стремится к нулю.

   Такого вида предел в математике называется производной функции по аргументу.

   - это есть изменение радиус-вектора движущейся точки, то есть функцией является радиус-вектор , а аргументом является время t. - изменение аргумента, следовательно, мгновенная скорость есть производная радиус-вектора движущейся точки по времени:

   (читается: "дэ-эр-по-дэ-тэ").

Итак:     .

Определение. Скорость точки в данное мгновение есть производная от радиус-вектора по времени.

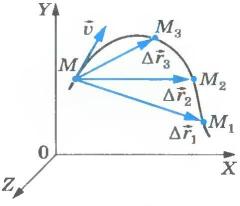
   Вектор мгновенной скорости направлен по касательной к траектории.

   Из математики знаем, что всякая производная характеризует быстроту изменения функции. Из этого следует физический смысл мгновенной скорости:

мгновенная скорость показывает быстроту изменения радиус-вектора движения точки с течением времени.

2. Проекции мгновенной скорости и их смысл.

   Знаем, что , , . 

   Поэтому:

;

;

.

   Проекции мгновенной скорости переменного движения равны производным от координат по времени и характеризуют быстроту изменения координат с течением времени.

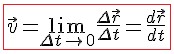< Предыдущий параграф <     Оглавление     > Следующий параграф >