ЛЕКЦИИ ПО ФИЗИКЕ
Некоторые сведения из математики

© Лопатин Павел Борисович
Настоящий курс лекций построен на основе лекций, которые читал Б.А. Слободсков.

§ 4. Нахождение вектора с помощью проекций

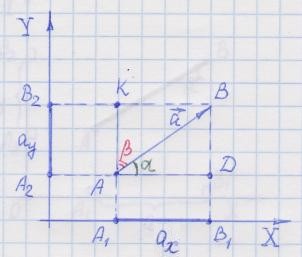
   Мир устроен так, что при познании Природы и создании технических устройств мы путём измерений получаем числа. Числа - не векторные величины. Но многие физические величины, например, такие как скорость или сила, являются векторными. Следовательно, надо уметь с помощью чисел находить векторы. Такими числами являются проекции вектора на оси координат.

   Найти вектор - это значит найти его модуль и направление. И осуществляется это с помощью проекций.

   Из прямоугольного треугольника ABD найдём модуль вектора по теореме Пифагора:

.

   Если была бы ещё ось OZ, то под корнем добавился бы квадрат проекции на ось OZ:

.

Правило 1. Модуль любого вектора равен квадратному корню из суммы квадратов проекций этого вектора на все оси координат.

   Направление вектора определяется углами, которые образует вектор с положительными направлениями осей координат.

   Из рисунка видно, что углы и определяют направление вектора ; их называют направляющими углами. Эти углы можно найти с помощью косинусов, а косинусы выражаются через проекции.
   Из треугольника ABD: .
   Из треугольника ABK: .

   Итак: .

Правило 2. Чтобы найти косинус угла, который образует вектор с положительным направлением оси координат, надо проекцию вектора на эту ось поделить на модуль вектора.

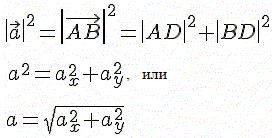   Определив направляющие косинусы, находят величины направляющих углов , и , которые образует вектор с осями координат.

< Предыдущий параграф <     Оглавление     > Следующий параграф >