ЛЕКЦИИ ПО ФИЗИКЕ
Некоторые сведения из математики

© Лопатин Павел Борисович
Настоящий курс лекций построен на основе лекций, которые читал Б.А. Слободсков.

§ 3. Проекции вектора на оси координат

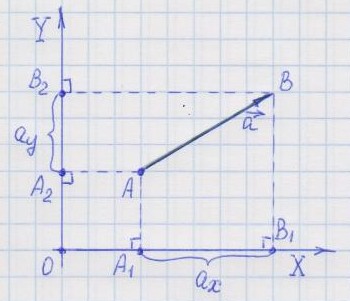
1. Нахождение проекций геометрически.

- вектор
- проекция вектора на ось OX
- проекция вектора на ось OY

Определение 1. Проекцией вектора на какую-либо ось координат называется взятое со знаком "плюс" или "минус" число, соответствующее длине отрезка, расположенного между основаниями перпендикуляров, опущенных из начала и конца вектора на ось координат.

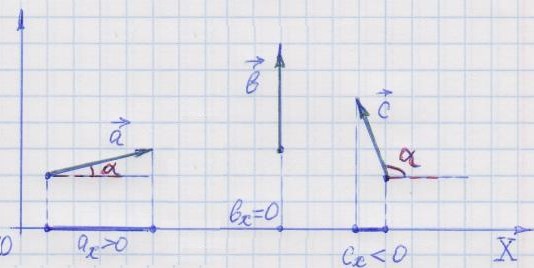
   Знак проекции определяется так. Если при движении вдоль оси координат происходит перемещение от точки проекции начала вектора к точке проекции конца вектора в положительном направлении оси, то проекция вектора считается положительной. Если же - противоположно оси, то проекция считается отрицательной.

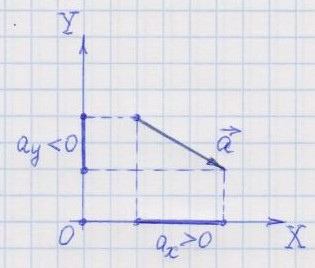
   По рисунку видно, что если вектор ориентирован как-то противоположно оси координат, то его проекция на эту ось отрицательна. Если вектор ориентирован как-то в положительном направлении оси координат, то его проекция на эту ось положительна.

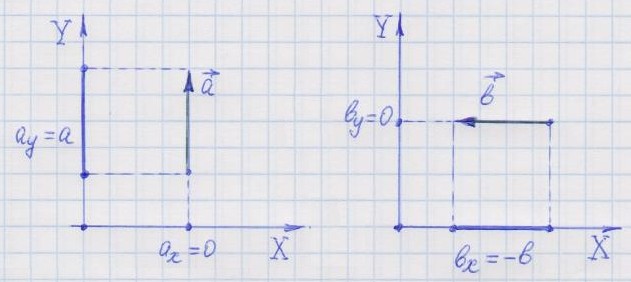
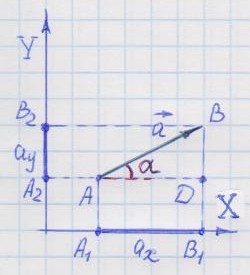
   Если вектор перпендикулярен оси координат, то его проекция на эту ось равна нулю.
   Если вектор сонаправлен с осью, то его проекция на эту ось равна модулю вектора.
   Если вектор противоположно направлен оси координат, то его проекция на эту ось по абсолютной величине равна модулю вектора, взятому со знаком минус.

2. Наиболее общее определение проекции.

Из прямоугольного треугольника ABD: .

Определение 2. Проекцией вектора на какую-либо ось координат называется число, равное произведению модуля вектора и косинуса угла, образованного вектором с положительным направлением оси координат.

   Знак проекции определяется знаком косинуса угла, образованного вектором с положительным направлением оси.
   Если угол острый, то косинус имеет положительный знак, и проекции - положительны. Для тупых углов косинус имеет отрицательный знак, поэтому в таких случаях проекции на ось отрицательны.
   - поэтому для векторов, перпендикулярных к оси, проекция равна нулю.

< Предыдущий параграф <     Оглавление     > Следующий параграф >