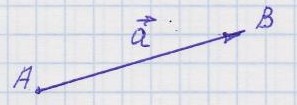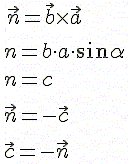ЛЕКЦИИ ПО ФИЗИКЕ
Некоторые сведения из математики

© Лопатин Павел Борисович
Настоящий курс лекций построен на основе лекций, которые читал Б.А. Слободсков.

§ 2. Некоторые сведения о векторах

1. Понятие о векторах и скалярах.

      Векторной величиной, или вектором (в широком смысле), называется всякая величина, обладающая направлением. Скалярной величиной, или скаляром, называется величина, не обладающая направлением.

      Пример 1. Скорость материальной точки есть вектор, так как она обладает направлением. Сила, действующая на материальную точку, - тоже вектор.

      Пример 2. Температура тела есть скаляр, так как с этой величиной не связано никакое направление. Масса тела и его плотность - тоже скаляры.

      Если отвлечься от направления векторной величины, то её, как и скалярную величину, можно измерить, выбрав соответствующую единицу измерения. Но число, полученное после измерения, характеризует скалярную величину полностью, а векторную - частично.

      Векторную величину можно полностью охарактеризовать направленным отрезком, предварительно задав линейный масштаб.

2. Вектор и его модуль.

- вектор

- модуль вектора

      Если вектор не геометрический, то его модулем называется длина вектора при заданном масштабе и выбранной единице измерения.
      Пример 3. На рисунке направленный отрезок АВ при масштабе MN, изображающем единицу силы (1 Н - один ньютон), характеризует силу в 3,5 Н, направление которой совпадает с направлением отрезка АВ (указанным стрелкой).

3. Равные векторы.

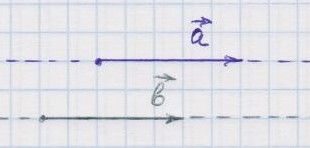
      Два вектора называются равными, если они сонаправлены, то есть имеют одинаковые направления, и равны по модулю.

4. Противоположные векторы.

      Векторы называются противоположными, если они имеют равные модули (длины), но противоположно направлены.

5. Коллинеарные векторы.

      Коллинеарные векторы - это векторы, которые лежат на параллельных прямых (или на одной и той же прямой) и имеют одно и то же направление или противонаправлены.

      Таким образом, равные и противоположные векторы являются коллинеарными. Но коллинеарные векторы необязательно должны иметь равную длину.

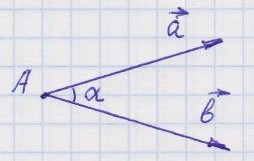
6. Для векторов не существует понятий "бо́льший" или "меньший", "положительный" или "отрицательный". Не существует таких понятий потому, что для векторов одинаково важны, как модуль, так и направление. Но для направления нет понятий "больше" или "меньше".

      Нет деления вектора на вектор.

7. Скалярное произведение векторов.

Определение. Скалярным произведением векторов называется произведение их модулей и косинуса угла между ними.

- обозначение скалярного произведения векторов

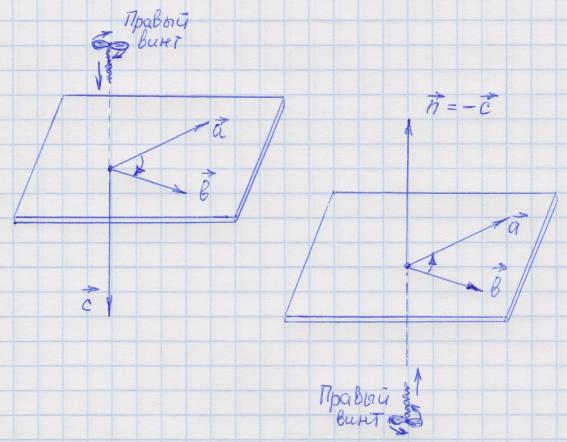
6. Векторное произведение векторов.

- обозначение векторного произведения

Определение. Векторным произведением двух векторов называется такой третий вектор, модуль которого равен произведению модулей перемножаемых векторов и синуса наименьшего угла между ними

а направление определяется с помощью правила правого винта. Винт с правой резьбой надо расположить перпендикулярно плоскости, на которой находятся перемножаемые векторы, и вращать его так, чтобы вращательное движение совпадало с переходом от первого сомножителя ко второму по наименьшему углу между ними; тогда поступательное движение оси винта укажет направление вектора векторного произведения.

      При перемене мест сомножителей в векторном произведении произведение изменяется на противоположное (см. рисунок выше).

< Предыдущий параграф <     Оглавление     > Следующий параграф >