ЛЕКЦИИ ПО ФИЗИКЕ
Кинематика

© Лопатин Павел Борисович
Настоящий курс лекций построен на основе лекций, которые читал Б.А. Слободсков.

§ 7. Три способа задания положения точки в пространстве

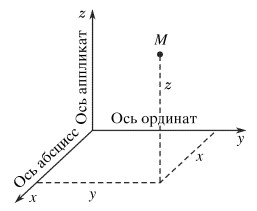
1. Координатный способ.

   Координаты определяют положение точки однозначно: например, M (x,y,z). Они являются числами, которые могут быть положительными, отрицательными или равными нулю.

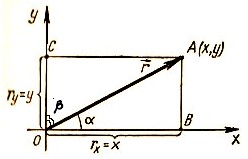
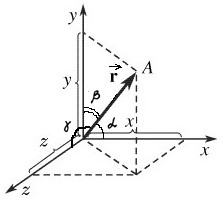
2. Векторный способ задания положения точки на плоскости и в пространстве.

Определение. Радиус-вектором  некоторой точки пространства называется вектор, проведённый из начала координат в данную точку пространства.

   Радиус-вектор также однозначно определяет положение точки в пространстве, так как он указывает, в каком направлении расположена точка, а модуль этого вектора указывает, на каком расстоянии находится точка от начала координат.

   Проекции радиуса-вектора на оси координат равны координатам конца этого вектора (см. рис. выше).

- модуль радиус-вектора

;  ;  - направляющие косинусы радиус-вектора

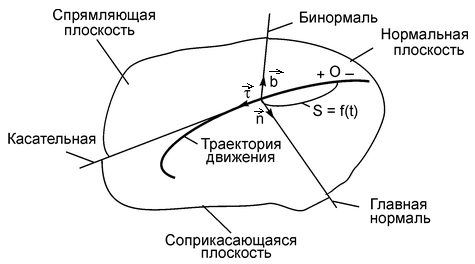
3. Естественный способ задания положения точки.

   Он применяется тогда, когда известна траектория, по которой движется точка.

   На траектории выбирают начало координат, а также положительное и отрицательное направление отсчёта дуговых координат. Векторные величины в этом случае проецируются на так называемые естественные оси координат: нормаль , касательную (тау), а также бинормаль .

   Начало естественных осей координат совмещают с той точкой траектории, через которую в данный момент проходит движущаяся точка. Касательную проводят в положительном направлении отсчёта дуг. Нормаль проводят перпендикулярно касательной и вовнутрь вогнутости траектории. Бинормаль направляют перпендикулярно плоскости, в которой расположены векторы  и , причём с конца вектора бинормали поворот от  к  по наименьшему углу между ними должен наблюдаться против часовой стрелки.

< Предыдущий параграф <     Оглавление     > Следующий параграф >